Angular Momentum, Rotational Motion, and Spin¶

In the previous notebooks, we discussed quantum mechanical problems involving translational and vibrational motion. In this notebook, we explore the properties of the operators corresponding to the angular momentum of a microscopic particle and model problems for rotational motion. We will find analytic solutions the Schrödinger equation for the particle-on-a-ring and particle-on-a-sphere models, which are models for rotational in two or three dimensions, respectively. The particle-on-a-sphere model is also known as the rigid rotor. We will also use an alternative approach based on "ladder" operators to find eigenvalues of some angular momentum operators. We close with a discussion of spin angular momentum and the associated spin operators and eigenfunctions.

Angular Momentum¶

Consider a particle of mass, $m$, with position $\vec{r} = (x, y, z)$ and linear momentum $\vec{p} = (p_x, p_y, p_z).$ The angular momentum for this particle is given by the cross product of the position and momentum vectors, i.e.,

$$ \begin{align} \vec{L} = (L_x, L_y, L_z) = \vec{r} \times \vec{p} \end{align} $$

The $x$, $y$, and $z$ components of the angular momentum are

$$ \begin{align} L_x &= y p_z - z p_y \\ L_y &= z p_x - x p_z \\ L_z &= x p_y - y p_x \end{align}$$

Given that $\hat{p}_x = -i\hbar \frac{\partial}{\partial x},$ etc., the corresponding angular momentum operators are

$$\begin{align} \hat{L}_x &= -i\hbar \left ( y \frac{\partial}{\partial z} - z \frac{\partial}{\partial y}\right ) \\ \hat{L}_y &= -i\hbar \left ( z \frac{\partial}{\partial x} - x \frac{\partial}{\partial z}\right ) \\ \hat{L}_z &= -i\hbar \left ( x \frac{\partial}{\partial y} - y \frac{\partial}{\partial x}\right ) \end{align}$$

We can also define an operator for the square of the angular momentum as

$$\begin{align} \hat{L}^2 = \hat{L} \cdot \hat{L} = \hat{L}_x^2 + \hat{L}_y^2 + \hat{L}_z^2 \end{align}$$

It will be useful to consider the commutator properties of these operators. If any commute, then it will be possible to determine simultaneous eigenfunctions of the operators, and, as a result, it will be possible to specify the corresponding observables simultaneously, with arbitrary precision. Let us begin with the commutator of $\hat{L}_x$ and $\hat{L}_z$:

$$ \begin{align} [\hat{L}_x, \hat{L}_y] f(x, y, z) = \hat{L}_x \hat{L}_y f(x, y, z) - \hat{L}_y \hat{L}_x f(x, y, z) \end{align}$$

For the first term on the right-hand side of this equation, we have

$$\begin{align} \hat{L}_y f &= -i\hbar \left ( z \frac{\partial f}{\partial x} - x\frac{\partial f}{\partial z} \right ) \\ \hat{L}_x \hat{L}_y f &= -\hbar^2 \left ( y \frac{\partial}{\partial z} - z \frac{\partial}{\partial y} \right ) \left ( z \frac{\partial f}{\partial x} - x\frac{\partial f}{\partial z} \right ) \\ &= -\hbar^2 \left ( y\frac{\partial f}{\partial x} + yz \frac{\partial^2 f}{\partial x \partial z} - xy \frac{\partial^2 f}{\partial z^2} - z^2 \frac{\partial^2 f}{\partial x \partial y} + xz \frac{\partial^2 f}{\partial y \partial z} \right ) \end{align}$$

For the second term, we have

$$\begin{align} \hat{L}_x f &= -i\hbar \left ( y \frac{\partial f}{\partial z} - z\frac{\partial f}{\partial y} \right ) \\ \hat{L}_y \hat{L}_x &= -\hbar^2 \left ( z \frac{\partial}{\partial x} - x \frac{\partial }{\partial z}\right ) \left ( y \frac{\partial f}{\partial z} - z\frac{\partial f}{\partial y} \right ) \\ &= -\hbar^2 \left ( yz \frac{\partial^2 f}{\partial x \partial z} - z^2 \frac{\partial^2 f}{\partial x \partial y} - xy \frac{\partial^2 f}{\partial z^2} + x \frac{\partial f}{\partial y} + xz \frac{\partial^2 f}{\partial y \partial z} \right ) \end{align}$$

Combining these results, most of the terms cancel, and the action of the commutator on $f(x,y,z)$ is simply

$$\begin{align} [\hat{L}_x, \hat{L}_y] f &= -\hbar^2 \left ( y \frac{\partial f }{\partial x} - x \frac{\partial f}{\partial y} \right ) \\ &= -\hbar^2 \left ( y \frac{\partial }{\partial x} - x \frac{\partial }{\partial y} \right ) f \\ &= i\hbar \hat{L}_z f \end{align}$$

Therefore,

$$ \begin{align} [\hat{L}_x, \hat{L}_y] = i\hbar \hat{L}_z \end{align}$$

Similarly, one could show that

$$ \begin{align} [\hat{L}_y, \hat{L}_z] &= i\hbar \hat{L}_x \\ [\hat{L}_z, \hat{L}_x] &= i\hbar \hat{L}_y \end{align}$$

Because these operators do not commute with one another, the Heisenberg uncertainty principle states that we cannot specify $L_x$ and $L_y$, $L_x$ and $L_z$, or $L_y$ and $L_z$ simultaneously, with arbitrary precision. Similarly, we cannot find a complete set of eigenfunctions of any pair of these operators.

Practice

Question 1. Show that $$ \begin{align} [\hat{L}_y, \hat{L}_z] = i\hbar \hat{L}_x \end{align}$$ and $$ \begin{align} [\hat{L}_z, \hat{L}_x] = i\hbar \hat{L}_y \end{align}$$

Now, consider the commutator of $\hat{L}^2$ and $\hat{L}_x$.

We have

$$ \begin{align} [\hat{L}^2, \hat{L}_x ] &= [\hat{L}_x^2 + \hat{L}_y^2 + \hat{L}_z^2, \hat{L}_x] \\ &= [\hat{L}_x^2, \hat{L}_x] + [\hat{L}_y^2, \hat{L}_x] + [\hat{L}_z^2, \hat{L}_x] \\ &= [\hat{L}_y^2, \hat{L}_x] + [\hat{L}_z^2, \hat{L}_x] \end{align}$$

where we are able to eliminate the first term because the commutator of an operator with itself is zero. It turns out that we can evaluate the remaining commutators with knowledge of the identity

$$ \begin{align} [\hat{A}\hat{B}, \hat{C}] = [\hat{A}, \hat{C}]\hat{B} + \hat{A}[\hat{B}, \hat{C}] \end{align}$$

For the commutator involving $\hat{L}_y^2$, we have

$$ \begin{align} [\hat{L}_y\hat{L}_y, \hat{L}_x] &= [\hat{L}_y, \hat{L}_x]\hat{L}_y + \hat{L}_y[\hat{L}_y, \hat{L}_x] \\ &= -i\hbar\hat{L}_z\hat{L}_y - i\hbar \hat{L}_y \hat{L}_z \end{align}$$

Similarly, the commutator involving $\hat{L}_z^2$ evaluates to

$$ \begin{align} [\hat{L}_z\hat{L}_z, \hat{L}_x] &= [\hat{L}_z, \hat{L}_x]\hat{L}_z + \hat{L}_z[\hat{L}_z, \hat{L}_x] \\ &= +i\hbar\hat{L}_y\hat{L}_z + i\hbar \hat{L}_z \hat{L}_y \end{align}$$

As a result,

$$ \begin{align} [\hat{L}^2, \hat{L}_x ] = 0 \end{align}$$

It turns out that $\hat{L}^2$ will commute with any cartesian component of the angular momentum operator, i.e.,

$$ \begin{align} [\hat{L}^2, \hat{L}_x ] = [\hat{L}^2, \hat{L}_y ] = [\hat{L}^2, \hat{L}_z ] = 0 \end{align}$$

As a result, there exists a complete set of eigenfunctions of both $\hat{L}^2$ and one cartesian component of the angular momentum operator. According to the Heisenberg uncertainty principle, this result also suggests that it is possible to specify simultaneously, with arbitrary precision, both the square of the angular momentum ($L^2$) and the $x$-component of the angular momentum vector, $L_x$ (or $L^2$ and $L_y$ or $L^2$ and $L_z$).

Practice

Question 2. Show that $$ \begin{align} [\hat{L}^2, \hat{L}_y] = 0 \end{align}$$ and $$ \begin{align} [\hat{L}^2, \hat{L}_z] = 0 \end{align}$$

Spherical Polar Coordinates¶

The spherical polar coordinate depicted below is the most natural coordinate system for describing rotational motion.

In [1]:

from IPython.display import Image
Image(url = "https://raw.githubusercontent.com/deprincelab/deprincelab.github.io/main/tutorials/jupyter_notebooks/rotation/spherical_polar_coordinates.png", width=300)

Out[1]:

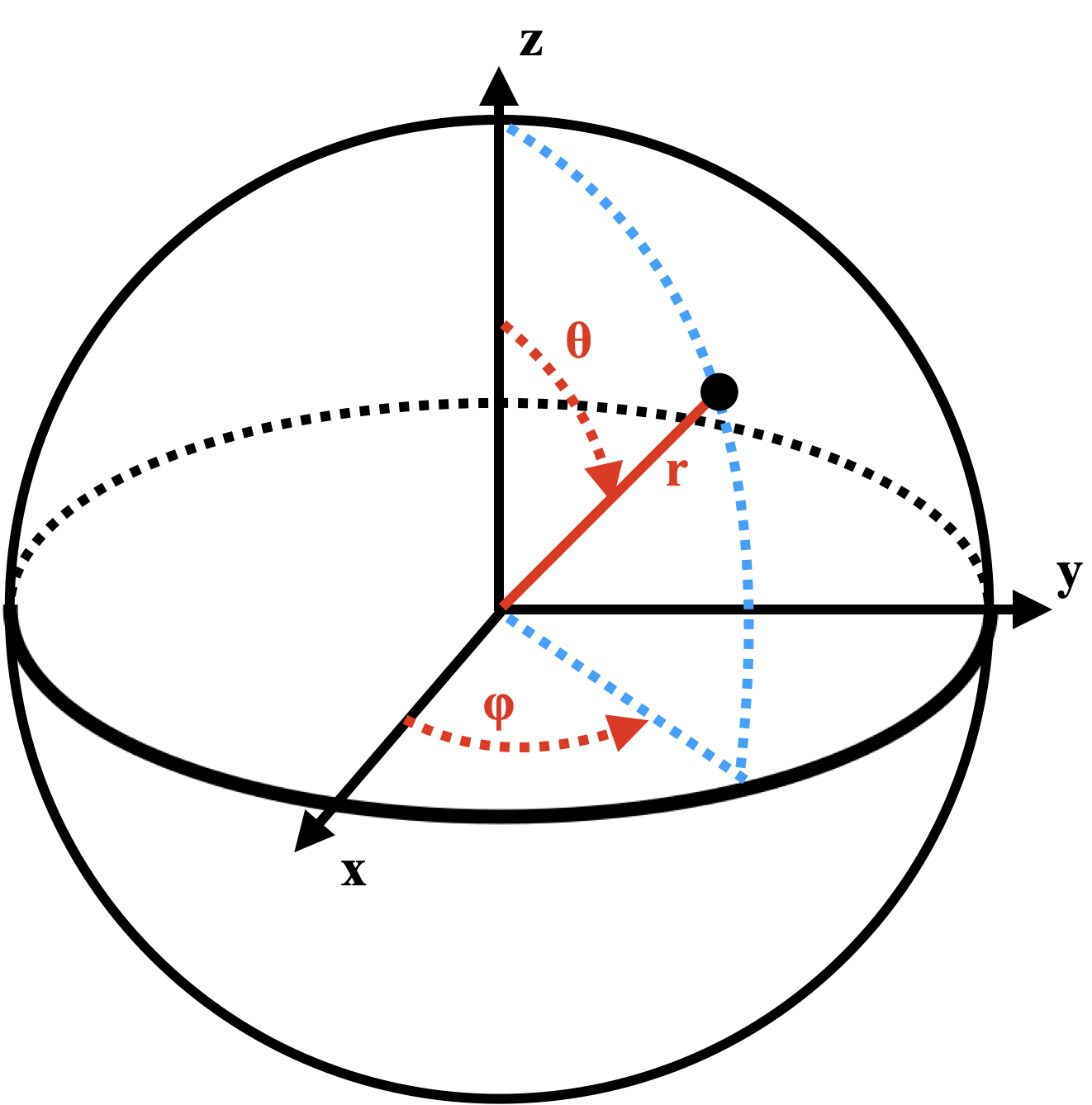
No description has been provided for this image

Here, $r$, represents the distance from the origin and spans the range $r = [0, \infty]$. The angle, $\phi$, is the azimuthal angle, which spans the range $\phi = [0, 2\pi]$ radians. The angle, $\theta$, is the polar angle, which spanse the range $\theta = [0, \pi]$ radians. The spherical polar coordinates are related to the usual Cartesian coordinates by

$$\begin{align} x &= r \sin(\theta)\cos(\phi) \\ y &= r \sin(\theta)\sin(\phi) \\ z &= r \cos(\theta) \\ r &= \left ( x^2 + y^2 + z^2 \right )^{1/2} \end{align}$$

In order to represent quantum mechanical operators in spherical polar coordinates, we first write down the operator in Cartesian coordinates and then use the relations above, as well as the chain rule to transform any derivatives. For the partial derivative with respect to $x$, we have

$$ \begin{align} \frac{\partial }{\partial x} &= \left (\frac{\partial r}{\partial x} \right )_{y,z} \frac{\partial }{\partial r} + \left (\frac{\partial \theta}{\partial x} \right )_{y,z} \frac{\partial }{\partial \theta} + \left (\frac{\partial \phi}{\partial x} \right )_{y,z} \frac{\partial }{\partial \phi} \\ &= \sin(\theta)\cos(\phi)\frac{\partial}{\partial r} + \frac{\cos(\theta)\cos(\phi)}{r}\frac{\partial}{\partial\theta}-\frac{\sin(\theta)}{r\sin(\theta)}\frac{\partial}{\partial \phi} \end{align}$$

Similarly, for the partial derivative with respect to $y$, we have

$$ \begin{align} \frac{\partial }{\partial y} &= \left (\frac{\partial r}{\partial y} \right )_{x,z} \frac{\partial }{\partial r} + \left (\frac{\partial \theta}{\partial y} \right )_{x,z} \frac{\partial }{\partial \theta} + \left (\frac{\partial \phi}{\partial y} \right )_{x,z} \frac{\partial }{\partial \phi} \\ &= \sin(\theta)\sin(\phi)\frac{\partial}{\partial r} + \frac{\cos(\theta)\sin(\phi)}{r}\frac{\partial}{\partial\theta}+\frac{\cos(\theta)}{r\sin(\theta)}\frac{\partial}{\partial \phi} \end{align}$$

Lastly, for the partial derivative with respect to $y$, we have

$$ \begin{align} \frac{\partial }{\partial z} &= \left (\frac{\partial r}{\partial z} \right )_{y,z} \frac{\partial }{\partial r} + \left (\frac{\partial \theta}{\partial z} \right )_{y,z} \frac{\partial }{\partial \theta} + \left (\frac{\partial \phi}{\partial z} \right )_{y,z} \frac{\partial }{\partial \phi} \\ &= \cos(\theta)\frac{\partial}{\partial r} - \frac{\sin(\theta)}{r}\frac{\partial}{\partial \theta} \end{align}$$

Given these results, we can express the angular momentum operators in spherical coordinates as

$$\begin{align} \hat{L}_x &= i\hbar \left [ \sin(\phi)\frac{\partial}{\partial \theta} + \cot(\theta)\cos(\phi)\frac{\partial}{\partial\phi} \right ]\\ \hat{L}_y &= -i\hbar \left [ \cos(\phi)\frac{\partial}{\partial \theta} - \cot(\theta)\sin(\phi)\frac{\partial}{\partial\phi} \right ]\\ \hat{L}_z &= -i\hbar \frac{\partial}{\partial \phi} \end{align}$$

and $$\begin{align} \hat{L}^2 = -\hbar^2 \left [ \frac{\partial^2}{\partial \theta^2} + \cot(\theta)\frac{\partial}{\partial \theta} + \frac{1}{\sin^2(\theta)}\frac{\partial^2}{\partial \phi^2} \right ] \end{align}$$

Recall that, based on the commutator relations given above, we will be able to select simultaneous eigenfunctions of $\hat{L}^2$ and at most one of the cartesian components of the angular momentum operator. The simplicity of the operator $\hat{L}_z$, relative to $\hat{L}_x$ and $\hat{L}_y$, makes this operator a desirable target for the following analyses.

The Particle-on-a-Ring Model¶

Consider a particle of mass, $m$, constrained to move on a ring of fixed radius, $r$, in the $xy$ plane.

In [2]:

Image(url = "https://raw.githubusercontent.com/deprincelab/deprincelab.github.io/main/tutorials/jupyter_notebooks/rotation/particle_on_a_ring.png", width=300)

Out[2]:

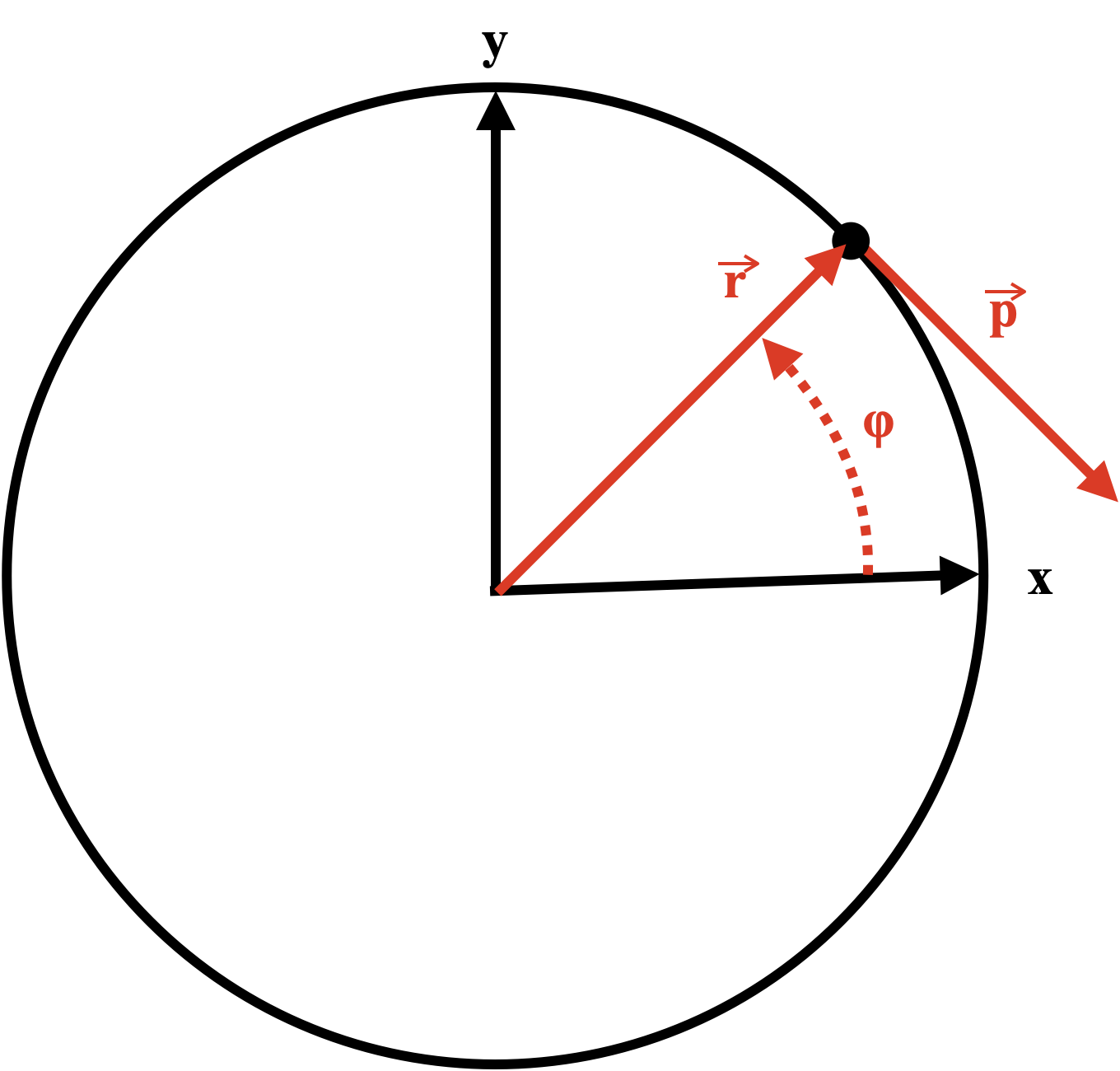
What would the angular momentum of a classical particle traveling on a ring be? Because the motion is constrained to the $xy$ plane, the $z$-components of the position, $\vec{r}$, and momentum, $\vec{p}$, are zero, and the angular momentum of the classical particle would thus be

$$\begin{align} \vec{L} = \vec{r} \times \vec{p} = (0, 0, L_z) \end{align}$$

where $L_z = x p_y - y p_x$

Let us determine the energy eigenfunctions for the quantum-mechanical particle on a ring. In order to do so, we must consider what sort of potential will constrain the particle to remain on the ring. We choose the potential such that it is zero when the particle is on the ring and infinite otherwise, so this problem resembles an angular version of the particle-in-a-box (PIB) problem. Like the PIB, the wave function will be zero in all regions of space where the potential is infinite, so we only consider the "region" of space corresponding to the ring. The Hamiltonian on the ring will be most compactly represented in spherical polar coordinates. Again, by applying the chain rule, we obtain

$$ \begin{align} \hat{H} &= \hat{T} \\ &= -\frac{\hbar^2}{2m} \nabla^2 \\ &= -\frac{\hbar^2}{2m}\left ( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \right ) \\ &= -\frac{\hbar^2}{2m}\left ( \frac{\partial^2}{\partial r^2} + \frac{2}{r}\frac{\partial}{\partial r} + \frac{1}{r^2}\left [ \frac{1}{\sin^2(\theta)}\frac{\partial^2}{\partial \phi^2} + \frac{1}{\sin(\theta)}\frac{\partial}{\partial \theta} \sin(\theta)\frac{\partial}{\partial \theta} \right ] \right ) \end{align} $$

The particle-on-a-rign energy eigenfunctions will be functions of the azimuthal angle, $\phi,$ only, so we can safely ignore all derivatives involving $r$ or $\theta$. The Laplacian, $\nabla^2$, then simplifies to

$$ \begin{align} \nabla^2 = \frac{1}{r^2}\left [ \frac{1}{\sin^2(\theta)}\frac{\partial^2}{\partial \phi^2} \right ] \end{align} $$

In the $xy$ plane, the polar angle, $\theta = \frac{\pi}{2}$, so $\sin^2(\theta) = 1$ and the Hamiltonian reduces to

$$ \begin{align} \hat{H} &= -\frac{\hbar^2}{2m} \frac{1}{r^2} \frac{\partial^2}{\partial \phi^2} \\ &= -\frac{\hbar^2}{2I} \frac{\partial^2}{\partial \phi^2} \end{align}$$

where we have introduced the moment of inertia, $I = mr^2.$ Interestingly, this Hamiltonian could also be expressed in terms of the operator for the $z$ component of the angular momentum, i.e.,

$$ \begin{align} \hat{H} = \frac{\hat{L}^2_z}{2I} \end{align}$$

Given this form for the Hamiltonian, is is clear that $\hat{H}$ and $\hat{L}_z$ will commute and we should thus be able to obtain simultaneous eigenfunctions of both operators.

Now, let us find solutions to the Schrödinger equation. We have

$$\begin{align} \hat{H} \psi(\phi) &= E \psi(\phi) \\ -\frac{\hbar^2}{2I} \frac{\partial^2}{\partial \phi^2} \psi(\phi) &= E \psi(\phi) \\ \frac{\partial^2}{\partial \phi^2} \psi(\phi) &= -\frac{2IE}{\hbar^2} \psi(\phi) \end{align}$$

A possible solution to this equation is

$$\begin{align} \psi(\phi) = A e^{ib\phi/\hbar} \end{align}$$

with $b = \left ( 2EI \right)^{1/2}$ or $E = \frac{b^2}{2I}$. This wave function is also an eigenfunction of $\hat{L}_z$

$$\begin{align} \hat{L}_z \psi(\phi) &= -i\hbar \frac{\partial}{\partial \phi} A e^{ib\phi/\hbar} \\ &= b A e^{ib\phi/\hbar} \end{align}$$

So, we have $L_z = b$ and $E = \frac{b^2}{2I} = \frac{L_z^2}{2I}.$ Note that the sign of $b$ provides information regarding the direction of rotation. A positive value of $b$ indicates that the rotation is clockwise, when viewing the ring from below. A negative value of $b$ indicates that the rotation is counter-clockwise, when viewing the ring from below.

Practice

Question 3. Show that $\psi(\phi) = C e^{ib\phi/\hbar} + D e^{-ib\phi/\hbar}$ is a solution to the Schrödinger equation for the particle-on-a-ring problem. What is the energy?

Question 4. Show that $\psi(\phi) = C e^{ib\phi/\hbar} + D e^{-ib\phi/\hbar}$ is not an eigenfunction of the operator, $\hat{L}_z$.

What boundary conditions should be satisfied by $\psi(\phi) = A e^{ib\phi/\hbar}$? Because the coordinate system is periodic in $\phi$, we must be careful to ensure that the wave function is single valued. We have

$$ \begin{align} \psi(\phi) &= \psi(\phi + 2\pi) \\ Ae^{ib\phi/\hbar} &=Ae^{ib(\phi + 2\pi)/\hbar} \\ &= Ae^{ib\phi/\hbar} e^{i 2\pi b/\hbar} \end{align} $$

$$ \begin{align} 1 &= e^{i 2\pi b/\hbar} \\ &= \cos\left(\frac{2\pi b}{\hbar}\right ) + i\sin\left(\frac{2\pi b}{\hbar}\right ) \end{align} $$

To satisfy this equation, the cosine term must be equal to one, and the sine term must be equal to zero. These conditions are satisfied by the choice

$$ \begin{align} \frac{2\pi b}{\hbar} = m 2 \pi \end{align} $$ or $b = m\hbar$, where $m = 0, \pm 1, \pm 2,$ etc. Now, after the application of this boundary condition, we can see that the energy for a particle-on-a-ring system in the state

$$ \begin{align} \psi_m(\phi) = A e^{im\phi} \end{align}$$

is quantized

$$ \begin{align} E_m = \frac{m^2\hbar^2}{2I} \end{align}$$

where we have added the subscripts to indicate that the state can be characterized by the quantum number $m$. In addition to the energy, the $z$ component of the angular momentum is also quantized

$$ \begin{align} L_z = m \hbar \end{align}$$

The quantization of a spatial quantity such as $L_z$ is called space quantization.

Before moving on, we note that we can determine the unknown coefficient, $A$, via normalization:

$$ \begin{align} 1 &= \int_0^{2\pi} |\psi_m(\phi)|^2 d\phi \\ &= |A|^2 \int_0^{2\pi} e^{-im\phi} e^{im\phi} d\phi \\ &= |A|^2 \int_0^{2\pi} d\phi \\ &= |A|^2 2\pi \end{align} $$

Taking $A$ to be real-valued, we have $A = (\frac{1}{2\pi})^{1/2}$ and

$$ \begin{align} \psi(\phi) = \left ( \frac{1}{2\pi} \right )^{1/2} e^{im\phi} \end{align}$$

The Particle-on-a-Sphere Model¶

Energies and Wave Functions¶

Consider a particle of mass, $m,$ confined to rotate on the surface of a sphere of fixed radius, $r$. Like in the particle-on-a-ring problem, the motion of the particle is constrained by a potential that is zero on the surface of the sphere and infinite elsewhere. The Hamiltonian in the region of space corresponding to the surface of the sphere is

$$ \begin{align} \hat{H} &= -\frac{\hbar^2}{2m} \nabla^2 \\ &= -\frac{\hbar^2}{2m}\left ( \frac{\partial^2}{\partial r^2} + \frac{2}{r}\frac{\partial}{\partial r} + \frac{1}{r^2}\left [ \frac{1}{\sin^2(\theta)}\frac{\partial^2}{\partial \phi^2} + \frac{1}{\sin(\theta)}\frac{\partial}{\partial \theta} \sin(\theta)\frac{\partial}{\partial \theta} \right ] \right ) \end{align} $$

This Hamiltonian can be expressed more compactly by recognizing that the parts involving the angular derivatives are actually related to $\hat{L}^2$, i.e,

$$ \begin{align} \hat{H} = -\frac{\hbar^2}{2m}\left ( \frac{\partial^2}{\partial r^2} + \frac{2}{r}\frac{\partial}{\partial r} \right ) + \frac{1}{2m r^2}\hat{L}^2 \end{align} $$

Like in the particle-on-a-ring problem, we ignore derivatives with respect to $r$ because the radius is fixed, and we are left with

$$ \begin{align} \hat{H} = \frac{1}{2I}\hat{L}^2 \end{align} $$

Now, it is evident that the eigenfunctions of the particle-on-a-sphere Hamiltonian are also eigenfunctions of the operator corresponding to the square of the angular momentum.

Recall that $\hat{L}^2$ commutes with $\hat{L}_z$. As such, we could choose to find solutions to the Schrödinger equation for the particle-on-a-sphere model that are simultaneous eigenfunctions of $\hat{L}^2$ and $\hat{L}_z$ that satisfy

$$ \begin{align} \hat{L}^2 Y(\theta,\phi) &= c Y(\theta,\phi) \\ \hat{L}_z Y(\theta,\phi) &= b Y(\theta,\phi) \end{align} $$

With infinite wisdom, we note that there is no $\theta$ dependence in $\hat{L}_z$, so it seems reasonable to expect that $Y(\theta, \phi)$ is factorizable into a product of functions that depend only on $\theta$ or $\phi.$ Let's try the form

$$ \begin{align} Y(\theta, \phi) = f(\theta) g(\phi) \end{align} $$

If we insert this form into the eigenvalue equation for $\hat{L}_z$, we obtain

$$ \begin{align} \hat{L}_z Y(\theta,\phi) &= b Y(\theta,\phi)\\ -i\hbar\frac{\partial}{\partial \phi} f(\theta) g(\phi) &= b f(\theta) g(\phi)\\ -i\hbar f(\theta) \frac{\partial}{\partial \phi} g(\phi) &= b f(\theta) g(\phi)\\ -i\hbar \frac{d g(\phi)}{d \phi} &= b g(\phi)\\ \end{align} $$

which, not surprisingly, is just an eigenvalue equation for $\hat{L}_z$, without any $\theta$ component. In the previous section, we found that the particle-on-a-ring energy eigenfunctions were also eigenfunctions of the $\hat{L}_z$, so we choose

$$ \begin{align} g(\phi) = \left ( \frac{1}{2\pi} \right )^{1/2} e^{im\phi} \end{align} $$

and

$$ \begin{align} Y(\theta, \phi) = \left ( \frac{1}{2\pi} \right )^{1/2} e^{im\phi} f(\theta) \end{align} $$

with $m = 0, \pm 1, \pm 2$, etc. Without the restriction on $m,$ the $phi$ component of $Y(\theta, \phi)$ would not be well behaved. Like we found for the particle-on-a-ring model, the eigenvalue $b$ is equal to $m\hbar$.

To find $f(\theta)$, we consider the eigenvalue equation for $\hat{L}^2$

$$ \begin{align} \hat{L}^2 \left ( \frac{1}{2\pi} \right )^{1/2} e^{im\phi} f(\theta) = c \left ( \frac{1}{2\pi} \right )^{1/2} e^{im\phi} f(\theta) \end{align} $$

which, after evaluating the action of $\hat{L}^2$ on $g(\theta)$ and collecting terms, gives

$$\begin{align} \frac{d^2}{d\theta^2} f(\theta) + \cot(\theta) \frac{d}{d\theta} f(\theta) - \frac{m^2}{\sin^2(\theta)}f(\theta) = -\frac{c}{\hbar^2} f(\theta) \end{align}$$

Solving this differential equation is quite complicated, so we will discuss the main points in the process. A detailed solution is given in Chapter 5 of Levine's Quantum Chemistry textbook. That text outlines several clever choices along the way to the solution, including a change of variables

$$\begin{align} \cos(\theta)& \to w\\ f(\theta) &\to f(w) \end{align} $$

and the introduction of an auxiliary function, $h(w)$, which is related to $f(w)$ by

$$\begin{align} f(w) = \left ( 1 - w^2 \right ) ^{|m|/2} h(w) \end{align}$$

The function $h(w)$ is expanded as a power series

$$ \begin{align} h(w) = \sum_{k=0}^\infty c_k w^k \end{align}$$

Inserting this form for $h(w)$ into the eigenvalue equation for $\hat{L}^2$ eventually leads to a two-term recursion relation for the expansion coefficients

$$\begin{align} c_{k+2} = \frac{\left [ (k + |m|)(k + |m| + 1) - \frac{c}{\hbar^2}\right ] }{(k+1)(k+2)} c_k \end{align}$$

Like in the quantum harmonic oscillator, inspection of various limits reveals that the $\hat{L}^2$ eigenfunctions are only well-behaved if the series expansion for $h(w)$ truncates (at $k_\text{max}$, for example). Then, we have

$$\begin{align} c = \hbar^2(k_\text{max} + |m|)(k_\text{max} + |m| + 1) \end{align}$$

$k_\text{max}$ corresponds to the upper limit in the series summation, so it must be a non-negative integer. Because $|m| = 0, 1, 2,$ etc. is also non-negative, the sum of these two quantities is non-negative and is a quantum number that characterizes the eigenfunctions of $\hat{L}^2$:

$$\begin{align} l = k_\text{max} + |m| = 0, 1, 2, ... \end{align}$$

and thus the square of the angular momentum for a particle confined to move on a sphere is quantized,

Note that this relationship also implies that $m$ is bounded by $l$, i.e.,

$$\begin{align} m = 0, \pm 1, \pm 2, ..., \pm l \end{align}$$

Now, we have

$$\begin{align} \hat{L}^2 Y(\theta, \phi) & = l(l+1) \hbar^2 Y(\theta, \phi)\\ \hat{L}_z Y(\theta, \phi) &= m \hbar Y(\theta, \phi)\text{, }\\ \end{align}$$

and, inserting this result into the Schrödinger equation, we have

$$ \begin{align} \hat{H} Y(\theta, \phi) &= E Y(\theta, \phi) \\ &= \frac{1}{2I} \hat{L}^2 Y(\theta, \phi)\\ &= \frac{l(l+1)\hbar^2}{2I} Y(\theta, \phi)\\ \end{align} $$

At this point, it is clear that the energy, the square of the angular momentum, and the $z$ projection of the angular momentum for a particle constrained to move on the surface of a sphere are all quantized, with

$$ \begin{align} E &= \frac{l(l+1)\hbar^2}{2I} \\ L^2 &= l(l+1)\hbar^2 \\ L_z &= m\hbar \\ \end{align} $$

From these results, we can see that the energy depends only on the quantum number, $l,$ and, each energy level is $(2l+1)$-fold degenerate because, for each $l$, there are $2l+1$ possible values of the quantum number, $m.$

Because the states can be characterized $l$ and $m,$ we label the wave functions for these states as $Y(\theta, \phi) \to Y^m_l(\theta, \phi).$ What is the form of these functions? We have

$$\begin{align} Y^m_l(\theta, \phi) &= \left ( \frac{1}{2\pi} \right )^{1/2} e^{im\phi} f(\theta) \end{align}$$

with

$$\begin{align} f(\theta) &= \sin^{|m|}(\theta)\sum_{j \in \{\text{odd or even}\}}^{l - |m|} c_j \cos^j(\theta) \end{align}$$ where the series expansion coefficients are determined by recursion. Note that the sum runs over even or odd non-negative integers depending on whether $k_\text{max} = l - |m|$ is even or odd. The sum must be restricted in this way to guarantee that the series truncates at $k_\text{max}.$ It turns out that $f(\theta)$ can be expressed in terms of special functions called associated Legendre polynomials, $\rho_l^{|m|},$

$$\begin{align} f(\theta) &= \left [ \frac{2l+1}{2}\frac{(l-|m|)!}{(l+|m|)!}\right ] \rho_l^{|m|}(\cos(\theta)) \end{align}$$

so the wave function is

$$\begin{align} Y^m_l(\theta, \phi) &= \left [ \frac{2l+1}{4\pi}\frac{(l-|m|)!}{(l+|m|)!}\right ] \rho_l^{|m|}(\cos(\theta))e^{im\phi} f(\theta) \end{align}$$

These special functions are known as the spherical harmonics. The spherical harmonics with up to $l=2$ are tabulated below.


$Y^0_0(\theta,\phi)$	$\frac{1}{2}\sqrt{\frac{1}{\pi}}$
$Y^0_1(\theta,\phi)$	$\frac{1}{2}\sqrt{\frac{3}{\pi}} \cos(\theta)$
$Y^{\pm 1}_1(\theta,\phi)$	$\mp\frac{1}{2}\sqrt{\frac{3}{2\pi}} e^{\pm i \phi}\sin(\theta)$
$Y^0_2(\theta,\phi)$	$\frac{1}{4}\sqrt{\frac{5}{\pi}}\left (3 \cos^2(\theta)-1\right)$
$Y^{\pm 1}_2(\theta,\phi)$	$\mp\frac{1}{2}\sqrt{\frac{15}{2\pi}}e^{\pm i \phi}\sin(\theta) \cos(\theta)$
$Y^{\pm 2}_2(\theta,\phi)$	$\frac{1}{4}\sqrt{\frac{15}{2\pi}}e^{\pm 2i \phi}\sin^2(\theta)$

Vector Diagrams¶

Vector diagrams allow us to visualize how the angular momentum vector is oriented in space. Consider a particle in a state represented by $Y^m_l(\theta, \phi).$ The magnitude of the total angular momentum is determined by the quantum number, $l$, i.e., $|L| = [l(l+1)\hbar^2]^{1/2},$ while the $z$ projection of the angular momentum is determined by the quantum number, $m.$ These quantities can be visualized for the $l=0, 1, 2, 3$ states with the following Python code

In [3]:

import numpy as np
import matplotlib.pyplot as plt
fig, (ax0, ax1, ax2, ax3) = plt.subplots(1, 4)

ax = []
ax.append(ax0)
ax.append(ax1)
ax.append(ax2)
ax.append(ax3)

# l = 0, 1, 2, 3
for l in range (0, 4):
    magnitude = np.sqrt(l * (l + 1))
    # m = -l ... l
    for m in range (-l, l+1): 
        dx = np.sqrt(magnitude*magnitude - m*m)
        dy = m
        ax[l].arrow(0, 0, dx, dy, head_width = 0.15, length_includes_head = True)
        ax[l].arrow(0, dy, dx, 0, linestyle = 'dotted', linewidth = 0.5)

    ax[l].set_ylim(-4, 4)
    ax[l].set_xlim(0, 4)
    
ax0.set_ylabel(r'z (units of $\hbar$)')

Out[3]:

Text(0, 0.5, 'z (units of $\\hbar$)')

From this figure, we can make the following observations:

The ground state ($l=0$) is a state for which the particle has zero angular momentum.
For all states with $l>0,$, there are $2l+1$ different states with different $m$ values. The magnitude of the angular momentum is the same for each of these states (as is the energy), but the direction in which the angular momentum vector points is different.
The $z$ projection of the angular momentum is quantized. This space quantization is at odds with the classical picture of angular momentum in a classical rotating body. However, we can see that the number of possible $z$ projections increases with $l$. In the limit that $l$ becomes large, the $z$ projection of the angular momentum becomes effectively continuous. This result is another manifestation of the Bohr Correspondence Principle.

This vector diagram is informative, but it is misleading in the sense that it makes it appear as though, in addition to knowledge regarding the magnitude and $z$ projection of the angular momentum vector, we also know something about its $x$ or $y$ component, depending on what the $x$ axis in the figure above is meant to represent. In reality, we can know nothing about the $x$ and $y$ components of the angular momentum vector because we know exactly what the $z$ component is and the relevant operators do not commute (although, the $l=0$ state is a special case which we will consider below). In reality, the angular momentum vector should lie on the edge of a cone with known magnitude and $z$ projection, as the following Python code illustrates for the $l=1$ states.

In [5]:

fig = plt.figure()
ax = plt.axes(projection="3d")
ax.view_init(azim=-72)

l = 1
for m in range (-1, 2):
    radius = np.sqrt( l*(l+1) - m*m )
    x = np.linspace(-radius, radius, 500)
    y = np.sqrt(radius**2 - x**2)
    for i in range (0, len(x)): 
        val = abs(x[i]) / abs(x[-1])
        plt.plot([0, x[i]], [0, y[i]], [0, m], color = (val, val, val))
        plt.plot([0, x[i]], [0, -y[i]], [0, m], color = (val, val, val))

ax.xaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.yaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.zaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))

ax.zaxis.set_ticks(ticks=[-1, 0, 1])

ax.set_zlabel(r'z (units of $\hbar$)', rotation = 0, labelpad= -2)

plt.xticks(ticks = [])
plt.yticks(ticks = [])

plt.show()

A Note Regarding Uncertainty¶

The general form of the Heisenberg Uncertainty Principle states that the product of the uncertainties in observables $A$ and $B$ is bounded by an expectation value involving the commutators of the corresponding operators. Specifically, we have

$$\begin{align} \Delta A \Delta B \ge \frac{1}{2} | \langle [\hat{A}, \hat{B} ] \rangle| \end{align}$$

If this commutator is zero, then it is possible to specify a complete set of common eigenfunctions of $\hat{A}$ and $\hat{B}$. Conversely, if these operators do not commute, then no such set of eigenfunctions exist, and it will not be possible, in general, to specify both $A$ and $B$ exactly, simultaneously.

For a particle constrained to move on a sphere in a state described by $Y^m_l(\theta, \phi),$ the product of the uncertainties in the $x$ and $y$ projections of the angular momentum would be

$$\begin{align} \Delta L_x \Delta L_y &\ge \frac{1}{2} \left | \langle Y^m_l(\theta, \phi) | [\hat{L}_x, \hat{L}_y] | Y^m_l(\theta, \phi) \rangle \right | \\ &= \frac{\hbar}{2} \left | \langle Y^m_l(\theta, \phi) | \hat{L}_z | Y^m_l(\theta, \phi) \rangle \right | \end{align}$$

Because $\hat{L}_x$ and $\hat{L}_y$ do not commute, it is impossible to find a complete set of common eigenfunctions for both operators. Is it ever possible to specify the $x$ and $y$ components of the angular momentum, simultaneously, with arbitrary precision? Surprisingly, the answer to this question is yes, but only in a single special case. Consider the state with $l=0$ and $m=0$. This is a state with zero total angular momentum and, obviously, zero $z$ projection of angular momentum. Because the total angular momentum is zero, the $x$ and $y$ projections must be exactly equal to zero, too! This result implies that the function $Y^0_0(\theta, \phi)$ is an eigenfunction of all four operators, $\hat{L}^2$, $\hat{L}_x$, $\hat{L}_y$, and $\hat{L}_z.$ The existence of a single common eigenfunction of these operators does not contradict the Heisenberg Uncertainty Principle, though. It is still impossible to specify a complete set of common eigenfunctions for these operators.

The Rigid Rotor¶

The particle-on-a-sphere model is equivalent to a model for molecular rotations known as the rigid rotor. In this section, we derive the Hamiltonian for the rigid-rotor problem and show the equivalence of these two models.

Consider two particles of mass $m_1$ and $m_2$ moving in three dimensions with coordinates $\vec{r}_1$ and $\vec{r}_2.$ The Hamiltonian for this system depends on the coordinates of both particles

$$\begin{align} \hat{H} = -\frac{\hbar^2}{2m_1}\nabla_1^2 - \frac{\hbar^2}{2m_1}\nabla_2^2 + V(\vec{r}) \end{align}$$

where $V(\vec{r})$ is a potenial that depends on the inter-particle separation

$$\begin{align} \vec{r} = \vec{r}_2 - \vec{r}_1 \end{align}$$

As written, this Hamiltonian is not separable in the coordinates of the particles, but we can obtain a separable Hamiltonian through a coordinate transformation. First, we introduce the center-of-mass coordinate, $\vec{R},$ defined as

$$\begin{align} \vec{R} = \frac{m_1 \vec{r}_1 + m_2 \vec{r}_2}{m_1 + m_2} \end{align}$$

which can be re-expressed in terms of the coordinates of one of the particles and $\vec{r}$ as

$$\begin{align} \vec{R} = \frac{m_1 \vec{r}_1 + m_2 (\vec{r}+\vec{r}_1)}{m_1 + m_2} \end{align}$$

Now, we introduce the total and reduced masses, $M$ and $\mu,$ respectively, which are defined by

$$\begin{align} M &= m_1 + m_2 \\ \mu &= \frac{m_1 m_2}{m_1 + m_2} \end{align}$$

From the expression for the center-of-mass cordinate, we have

$$\begin{align} M \vec{R} = M \vec{r}_1 + m_2 \vec{r} \end{align}$$

We can also express $\vec{r}_1$ and $\vec{r}_2$ in terms of $\vec{R}$ and $\vec{r}$ as

$$\begin{align} \vec{r}_1 &= \vec{R} - \frac{m_2}{M} \vec{r} \\ \vec{r}_2 &= \vec{R} + \frac{m_1}{M} \vec{r} \end{align}$$

Now, what happens to the classical expression for the kinetic energy with these new coordinates? We begin with the momenta for these particles, defined by

$$\begin{align} \vec{p}_i = m_i \frac{d \vec{r}_i}{dt} = m_i \dot{r}_i \end{align}$$

The kinetic energy is then

$$\begin{align} T &= \frac{\vec{p}_1\cdot \vec{p}_1}{2 m_1} + \frac{\vec{p}_2 \cdot \vec{p}_2}{2 m_2}\\ &= \frac{m_1}{2} \dot{\vec{r}}_1 \cdot \dot{\vec{r}}_1 + \frac{m_2}{2} \dot{\vec{r}}_2 \cdot \dot{\vec{r}}_2 \\ &= \frac{m_1}{2} \left ( \dot{\vec{R}} - \frac{m_2}{M}\dot{\vec{r}} \right ) \cdot \left ( \dot{\vec{R}} - \frac{m_2}{M}\dot{\vec{r}} \right ) \nonumber \\ &+ \frac{m_2}{2} \left ( \dot{\vec{R}} + \frac{m_1}{M}\dot{\vec{r}} \right ) \cdot \left ( \dot{\vec{R}} + \frac{m_1}{M}\dot{\vec{r}} \right ) \\ &= \frac{m_1 + m_2}{2} \dot{\vec{R}} \cdot \dot{\vec{R}} + \frac{m_1 m_2}{2 M} \dot{\vec{r}}\cdot \dot{\vec{r}} \\ &= \frac{M}{2} \dot{\vec{R}} \cdot \dot{\vec{R}} + \frac{\mu}{2} \dot{\vec{r}}\cdot \dot{\vec{r}} \\ &= \frac{\vec{p}_M \cdot \vec{p}_M}{2M} + \frac{\vec{p}_\mu \cdot \vec{p}_\mu}{2\mu} \end{align}$$

where $\vec{p}_M$ and $\vec{p}_\mu$ are momenta for effective particles of mass $M$ and $\mu$ that depend on the coordinates $\vec{R}$ and $\vec{r},$ respectively. We can define quantum mechanical operators for these momenta and insert them into the Hamiltonian to obtain

$$\begin{align} \hat{H} = \frac{\hat{p}_M^2}{2M} + \left [ \frac{\hat{p}_\mu^2}{2\mu} + V(\vec{r}) \right ] \end{align}$$

The first term depends on the center-of-mass coordinate $(\vec{R}),$ while the second and third terms depend on the inter-particle separation coordinate $(\vec{r}).$ With this choice of coordinates, the Hamiltonian is additively separable. As a result, the wave function can be expressed as a product of wave functions for effective particles of mass $M$ and $\mu$

$$ \begin{align} \psi(\vec{R}, \vec{r}) = \psi_M(\vec{R}) \psi_\mu(\vec{r}) \end{align}$$

and the energy will be expressible as a sum

$$ \begin{align} E = E_M + E_\mu \end{align}$$

Because the Hamiltonian is separable, these wave function and energy components can be obtained by solving separate Schrödinger equations that involve only one coordinate, i.e.,

$$\begin{align} \hat{H}_M \psi_M(\vec{R}) &= E_M \psi_M(\vec{R}) \\ \hat{H}_\mu \psi_\mu(\vec{r}) &= E_\mu \psi_\mu(\vec{r}) \end{align}$$

where

$$\begin{align} \hat{H}_M &= \frac{\hat{p}_M^2}{2M} \\ \hat{H}_\mu &= \frac{\hat{p}_\mu^2}{2\mu} + V(\vec{r}) \end{align}$$

The first of these equations resembles the Schrödinger equation for a free-particle of mass, $M.$ As such, the energy, $E_M,$ corresponds to the translational energy of the entire system traveling through space and will not be quantized. The Schrödinger equation for the effective particle of mass, $\mu,$ is more complicated, and its solution will depend on the precise form of $V(\vec{r}).$ Depending on the form of this potential, $E_\mu$ may be quantized.

To this point, this analysis has been completely general. The Hamiltonian for any two-particle system with a potential that depends on the inter-particle distance can be separated in this way. The $\vec{R}$-dependent part of the wave function will always look like that for a free-particle, where as the $\vec{r}$-dependent part will be more interesting. Here, we are specifically concerned with the case where $\psi(\vec{r})$ is a wave function characterizing the rotational motion of a molecular system (specifically, a diatomic molecule). In the rigid rotor model, the atoms in this molecular are assumed to rotate about their center of mass, at a fixed distance, $d$ from one-another. As a result $V(\vec{r})$ is chosen to be zero when $|\vec{r}|=d$ and infinite otherwise. This potential is sperically symmetrical, meaning that it depends on the magnitude but not the orientation of $\vec{r}.$ For a particle experiencing such a potential, the force experienced by the particle is radially directed. For this reason, this type of a problem is called a central force problem.

Practice

Question 5.

Show that the force for a central force problem is

$$\begin{align}\vec{f} = -\frac{d V(r)}{dr} \frac{\vec{r}}{r}\end{align}$$

where $r = |\vec{r}|.$

It turns out that the wave function for a central force problem is separable as

$$\begin{align} \psi_\mu(\vec{r}) &= \psi_\mu(r, \theta, \phi) \\ &= R(r) Y^m_l(\theta, \phi) \end{align}$$

where $R(r)$ is a radial wave function, and $Y^m_l(\theta, \phi)$ are the same spherical harmonics that are eigenfunctions of the orbital angular momentum operators, $\hat{L}^2$ and $\hat{L}_z.$ Now, because $r$ is fixed in the rigid rotor problem, the function $R(r)$ has no meaning and is ignored. We are left with

$$\begin{align} \psi_\mu(\theta, \phi) &= Y^m_l(\theta, \phi) \end{align}$$

The Hamiltonian for the rigid rotor is the $\mu$-dependent part of the Hamiltonian above. If we consider only the region of space where $|\vec{r}| = r = d,$ where the potential, $V(\vec{r}),$ vanishes, then we have

$$ \begin{align} \hat{H}_\mu = -\frac{\hbar^2}{2\mu}\left ( \frac{\partial^2}{\partial r^2} + \frac{2}{d}\frac{\partial}{\partial r} \right ) + \frac{1}{2\mu d^2}\hat{L}^2 \end{align} $$

Note that, because $r$ is fixed, we have replaced it with $d$ in this expression. Moreover, with $r$ being fixed, derivatives with respect to $r$ carry no meaning, so we ignore these terms and are left with

$$ \begin{align} \hat{H}_\mu = \frac{1}{2\mu d^2}\hat{L}^2 \end{align} $$

The corresponding Schrödinger equation is

$$\begin{align} \hat{H}_\mu \psi_\mu &= E_\mu \psi_\mu \\ \frac{1}{2\mu d^2}\hat{L}^2 Y^m_l &= E_\mu Y^l_m \\ &= \frac{l(l+1)\hbar^2}{2\mu d^2} Y^l_m \end{align}$$

So, the energy for a two-particle rigid rotor is quantized and given by

$$\begin{align} E &= \frac{l(l+1)\hbar^2}{2\mu d^2} \\ &= \frac{l(l+1)\hbar^2}{2I} \end{align} $$

where $I = \mu d^2$ is the moment of inertia for the molecule. As was the case for the particle-on-a-sphere model, the rotational quantum number, $l,$ can take on any non-negative integer, and $m$ is bounded by $l$

$$ \begin{align} l &= 0, 1, 2, ... \\ m &= 0, \pm 1, \pm 2, ... \pm l \end{align}$$

As such, each energy level is $(2l+1)$-fold degenerate.

Note that this result is generalizable to rotating molecules with more than two atoms. Rotational energy levels are given by the energy expression above, augmented by the appropriate moment of inertia.

Selection Rules¶

The rigid rotor model can be used to predict both rotational energy levels and spectra for rotations in molecules. Here, we derive rules for which rotational transitions will be "allowed" or "forbidden."

Fermi's Golden Rule for Molecular Rotations

Recall that Fermi's Golden Rule allows us to predict the probability that a system will transition between energy states when interacting with a time-dependent external perturbation. For a rigid rotor interacting with an oscillating electric field, a transition between states characterized by the wave functions $Y^m_l(\theta, \phi)$ and $Y^{m^\prime}_{l^\prime}(\theta, \phi)$ will be proportional to the square modulus of the transition dipole moment involving these wave functions,

$$\begin{align} P_{m,l \to m^\prime, l^\prime} \propto |\langle Y^m_l(\theta, \phi) | \hat{\mu} | Y^{m^\prime}_{l^\prime}(\theta, \phi) \rangle |^2 \end{align}$$

For the quantum harmonic oscillator model, we were able to derive selection rules from the recursion relations for Hermite polynomials. It turns out that we can derive selection rules for the rigid rotor that are related to the change in $m,$ $\Delta m = m - m^{\prime},$ from commutator relations involving the operators $\hat{L}_z$, $x,$, $y,$ and $z.$

Practice

Question 6.

Show that $[\hat{L}_z, x] = i\hbar y$

Question 7.

Show that $[\hat{L}_z, y] = -i\hbar x$

Question 8.

Show that $[\hat{L}_z, z] = 0$

Let us insert $[\hat{L}_z, z] = 0$ into an integral involving the states $Y^m_l$ and $Y^{m^\prime}_{l^\prime}$, where we suppress the notation for the dependence on the coordinates $\theta$ and $\phi$

$$\begin{align} \langle Y^m_l | [\hat{L}_z, z] | Y^{m^\prime}_{l^\prime} \rangle &= 0 \\ &= \langle Y^m_l | \hat{L}_z z | Y^{m^\prime}_{l^\prime} \rangle - \langle Y^m_l | z\hat{L}_z | Y^{m^\prime}_{l^\prime} \rangle \\ &= \langle Y^m_l | \hat{L}_z | f \rangle - m^\prime \hbar \langle Y^m_l | z | Y^{m^\prime}_{l^\prime} \rangle \\ &= \langle f | \hat{L}_z | Y^m_l \rangle^* - m^\prime \hbar \langle Y^m_l | z | Y^{m^\prime}_{l^\prime} \rangle \\ &= m^* \hbar \langle f | Y^m_l \rangle^* - m^\prime \hbar \langle Y^m_l | z | Y^{m^\prime}_{l^\prime} \rangle \\ &= m \hbar \langle Y^m_l | f \rangle - m^\prime \hbar \langle Y^m_l | z | Y^{m^\prime}_{l^\prime} \rangle \\ &= (m - m^\prime) \hbar \langle Y^m_l | z | Y^{m^\prime}_{l^\prime} \rangle \end{align}$$

Where, on the third line, we have introduced a function, $|f\rangle = z|Y^{m^\prime}_{l^\prime}\rangle$ to make the manipulation in the fourth line, based on the Hermiticity of the operator $\hat{L}_z$ a little easier to see. Note also that we also took advantage of the fact that $m$ is a real number, i.e., $m = m^*.$ Now, we are left with

$$\begin{align} (m - m^\prime) \langle Y^m_l | z | Y^{m^\prime}_{l^\prime} \rangle = 0 \end{align}$$

For $z$ polarized light, a transition between states $Y^m_l$ and $Y^{m^\prime}_{l^\prime}$ will only occur if the integral $\langle Y^m_l | z | Y^{m^\prime}_{l^\prime} \rangle$ is non-zero. If this integral is non-zero, then this equation can only be satisfied if

$$\begin{align} \Delta m = m - m^\prime = 0 \end{align}$$

If we perform a similar exercise involving the commutators $[\hat{L}_z, x]$ and $[\hat{L}_z, y],$ we would find two additional selection rules. In total, we have three selection rules for allowed changes in the $m$ quantum number:

$$\begin{align} \Delta m = 0, \pm 1 \end{align}$$

There is also a selection rule on the change in the quantum number, $l,$ that we will not derive:

$$\begin{align} \Delta l = \pm 1 \end{align}$$

In addition to these rules, non-zero transitions in "pure" rotational spectra (with no changes in vibrational energy levels) require that the molecule have a permanent dipole moment.

Practice

Question 9:

Derive the $\Delta m = \pm 1$ selection rules from the commutators $[\hat{L}_z, x]$ and $[\hat{L}_z, y]$

Ladder Operators¶

Above, we derived the eigenfunctions and eigenvalues of $\hat{L}^2$ and $\hat{L}_z$ by solving the respective eigenvalue equations. It turns out that we can also derive the eigenvalues for these operators using only their commutator properties. These results will also apply to other types of angular momentum whose operators have the same commutator properties, like spin angular momentum, so let us consider the following general angular momentum operators

$$\begin{align} \vec{M} &= \hat{M}_x \vec{i} + \hat{M}_y \vec{j} + \hat{M}_z \vec{k} \\ \hat{M}^2 &= \hat{M}_x^2 + \hat{M}_y^2 + \hat{M}_z^2 \\ \end{align}$$

We assume that these operators have similar commutator properties as we derived above, so

$$\begin{align} [\hat{M}^2, \hat{M}_x] &= 0 \\ [\hat{M}^2, \hat{M}_y] &= 0 \\ [\hat{M}^2, \hat{M}_z] &= 0 \\ [\hat{M}_x, \hat{M}_y] &= i\hbar \hat{M}_z \\ [\hat{M}_z, \hat{M}_x] &= i\hbar \hat{M}_y \\ [\hat{M}_y, \hat{M}_z] &= i\hbar \hat{M}_x \\ \end{align}$$

Now, we introduce "raising" and "lowering" operators, $\hat{M}_-$ and $\hat{M}_+,$ respectively, whose names will become clear soon.

$$\begin{align} \hat{M}_+ &= \hat{M}_x + i \hat{M}_y \\ \hat{M}_- &= \hat{M}_x - i \hat{M}_y \\ \end{align}$$

Do these operators commute with $\hat{M}_z$? Let's check.

$$\begin{align} [\hat{M}_+, \hat{M}_z ] &= [\hat{M}_+, \hat{M}_x + i \hat{M}_y] \\ &= [\hat{M}_+, \hat{M}_x] + i [\hat{M}_+, \hat{M}_y] \\ &= -i\hbar \hat{M}_y - \hbar\hat{M}_x \\ &= -\hbar \hat{M}_+ \end{align}$$

No! These operators do not commute, and neither do $\hat{M}_-$ and $\hat{M}_z.$ For that case, we have

$$\begin{align} [\hat{M}_-, \hat{M}_z ] &= +\hbar \hat{M}_- \end{align}$$

We can reexpress these commutator relations in a form that will soon become useful as

$$\begin{align} \hat{M}_+ \hat{M}_z &= \hat{M}_z \hat{M}_+ - \hbar \hat{M}_+ \\ \hat{M}_- \hat{M}_z &= \hat{M}_z \hat{M}_- + \hbar \hat{M}_- \end{align}$$

Practice

Question 10.

Show that $[\hat{M}_-, \hat{M}_z] = +\hbar \hat{M}_-$

Now, consider the eigenvalue equation for $\hat{M}_z$

$$\begin{align} \hat{M}_z Y = b Y \end{align}$$

and let us apply $\hat{M}_+$ on the left to both sides of this equation

$$\begin{align} \hat{M}_+ \hat{M}_z Y &= b \hat{M}_+ Y \\ \hat{M}_z \hat{M}_+ Y - \hbar \hat{M}_+ Y &= b \hat{M}_+ Y\\ \hat{M}_z (\hat{M}_+ Y) &= (b+\hbar) (\hat{M}_+ Y) \end{align}$$

Now, we see that the function $\hat{M}_+ Y$ is an eigenfunction of $\hat{M}_z$, with eigenvalue one unit of $\hbar$ higher than that for $Y,$ which is why we call $\hat{M}_+$ a "raising" operator. We could repeat this process multiple times to obtain

$$\begin{align} \hat{M}_z (\hat{M}^k_+ Y) &= (b+k\hbar) (\hat{M}^k_+ Y) \end{align}$$

A similar analysis involving $\hat{M}_-$ leads to

$$\begin{align} \hat{M}_z (\hat{M}^k_- Y) &= (b-k\hbar) (\hat{M}^k_- Y) \end{align}$$

Hence, $\hat{M}_\pm$ generate a "ladder" of eigenfunctions of $\hat{M}_z$, which is why we call such operators "ladder operators."

Now, does $\hat{M}^2$ commute with the raising and lowering operators? We have

$$\begin{align} [\hat{M}^2, \hat{M}_\pm ] = [\hat{M}^2, \hat{M}_x ] \pm i [\hat{M}^2, \hat{M}_y ] = 0 \end{align}$$

So, yes, these operators commute, and we thus have

$$\begin{align} \hat{M}^2 \hat{M}_\pm = \hat{M}_\pm \hat{M}^2 \end{align}$$

Now, consider the eigenvalue equation for $\hat{M}^2$

$$\begin{align} \hat{M}^2 Y = c Y \end{align}$$

Let us act on this equation with $\hat{M}_\pm^k$ on both sides

$$\begin{align} \hat{M}_\pm^k \hat{M}^2 Y &= c \hat{M}_\pm^k Y \\ \hat{M}^2(\hat{M}_\pm^k Y) &= c (\hat{M}_\pm^k Y) \end{align}$$

This result indicates that the function $\hat{M}_+ Y$ is an eigenfunction of $\hat{M}^2$ with the same eigenvalue as $Y.$ As such, each "rung" on the ladder generated by $\hat{M}_\pm^k$ is an eigenfunction of both $\hat{M}_z$ and $\hat{M}^2$.

Is there a limit to the number of times $\hat{M}_\pm$ can be applied to a state? Let us define a family of functions satisfying

$$\begin{align} \hat{M}_z Y_k = b_k Y_k \end{align}$$

where

$$\begin{align} Y_k &= \hat{M}^k_\pm Y_k \\ b_k &= b \pm k \hbar \end{align}$$

Now, if we act on the state $Y_k$ with the operator $\hat{M}^2 - \hat{M}_z$ we have

$$\begin{align} (\hat{M}^2 - \hat{M}_z)Y_k &= (c - b_k^2)Y_k \\ \end{align}$$

or, equivalently, based on how $\hat{M}^2$ was defined above

$$\begin{align} (\hat{M}_x^2 + \hat{M}^2_y)Y_k &= (c - b_k^2)Y_k \\ \end{align}$$

Multiplying this expression on the left by $Y_k^*$ and integrating over all space yields

$$\begin{align} \langle Y_k | \hat{M}_x^2 | Y_k \rangle + \langle Y_k | \hat{M}^2_y | Y_k\rangle &= (c - b_k^2)\langle Y_k | Y_k \rangle \\ \end{align}$$

The two integrals on the left-hand side of this equation represent expectation values of the square of an operator, the results of which much be non-negative. Similarly, the integral on the right-hand side of this expression is also non-negative. As such, we expect that the quantity $c-b_k^2$ must also be non-negative, which implies that

$$\begin{align} -c^{1/2} \le b_k \le c^{1/2} \end{align}$$

This result indicates that $b_k$ is bounded by $c.$ In other words, the ladder of functions $Y_k$ is finite!

If a bound on $b_k$ exists, our next goal should be to find the maximum / minimum allowed values of $b_k$ that satisfy

$$\begin{align} \hat{M}_z Y_\text{max} &= b_\text{max} Y_\text{max} \\ \hat{M}_z Y_\text{min} &= b_\text{min} Y_\text{min} \end{align}$$

To do so, we can consider the application of the raising operator to the top rung of the ladder:

$$\begin{align} \hat{M}_z (\hat{M}_+ Y_\text{max}) = (b_\text{max} + \hbar)(\hat{M}_+ Y_\text{max}) \end{align}$$

This result suggests that the state $\hat{M}_+ Y_\text{max}$ has a larger $z$ projection of the angular momentum than the state $Y_\text{max}$, which contradicts our assertion that $Y_\text{max}$ represents the top rung of the ladder of functions. To avoid this contridiction, the application of $\hat{M}_+$ to $Y_\text{max}$ must be zero:

$$\begin{align} \hat{M}_+Y_\text{max} = 0 \end{align}$$

We obtain a useful result if we probe this zero state with $\hat{M}_-$ as

$$\begin{align} \hat{M}_-\hat{M}_+Y_\text{max} &= 0 \\ &= (\hat{M}_x - i \hat{M}_y)(\hat{M}_x + i\hat{M}_y) Y_\text{max} \\ &= (\hat{M}_x^2 + \hat{M}_y^2 + i [M_x, M_y]) Y_\text{max} \\ &= (\hat{M}^2 - \hat{M}_z^2 - \hbar \hat{M}_z ) Y_\text{max} \\ &= (c - b_\text{max}^2 - \hbar b_\text{max}) Y_\text{max} \end{align}$$

where on the fourth line, we have made use of the commutator relation given above. Now, we can see that $c$ and $b_\text{max}$ should satisfy

$$\begin{align} c - b_\text{max}^2 - \hbar b_\text{max} = 0 \end{align}$$

$$\begin{align} c = b_\text{max}(b_\text{max} + \hbar) \end{align}$$

If we repeat this exercise starting with

$$\begin{align} \hat{M}_- Y_\text{min} = 0 \end{align}$$

which must be true to avoid a similar contradition as we encountered above, we obtain

$$\begin{align} \hat{M}_+\hat{M}_- Y_\text{min} &= 0 \\ &= (\hat{M}_x + i \hat{M}_y)(\hat{M}_x - i\hat{M}_y) Y_\text{min} \\ &= (\hat{M}_x^2 + \hat{M}_y^2 - i [M_x, M_y]) Y_\text{min} \\ &= (\hat{M}^2 - \hat{M}_z^2 + \hbar \hat{M}_z ) Y_\text{min} \\ &= (c - b_\text{min}^2 + \hbar b_\text{min}) Y_\text{min} \end{align}$$

which suggests

$$\begin{align} c = b_\text{min}^2 - \hbar b_\text{min} \end{align}$$

Subtracting this result from the other expression for $c$ in terms of $b_\text{max}$ gives

$$\begin{align} b_\text{max}^2 + \hbar b_\text{max} - b_\text{min}^2 + \hbar b_\text{min} = 0 \end{align}$$

which we can solve as a quadratic equation in $b_\text{max}$. This equation has two solutions

$$\begin{align} b_\text{max} &= \frac{-\hbar \pm \sqrt{\hbar^2 - 4(\hbar b_\text{min} - b_\text{min}^2)}}{2} \\ &= \frac{-\hbar \pm(\hbar - 2b_\text{min})}{2} \end{align}$$

which simplify to

$$\begin{align} b_\text{max} = -b_\text{min} \end{align}$$

and

$$\begin{align} b_\text{max} = b_\text{min} - \hbar \end{align}$$

We reject the second solution because $b_\text{max}$ must be greater than $b_\text{min}.$ Recall that

$$\begin{align} b_k = b \pm k\hbar \end{align}$$

where $k$ is an integer, which suggests that

$$\begin{align} b_\text{max} - b_\text{min} = n \hbar\text{, }~~~n = 0, 1, 2... \end{align}$$

Given that $b_\text{max} = -b_\text{min},$ we now see that

$$\begin{align} b_\text{max} - (-b_\text{max}) &= n\hbar \\ 2 b_\text{max} &= n \hbar\\ \end{align}$$

and

$$\begin{align} b_\text{max} &= \frac{n\hbar}{2} \\ b_\text{min} &= -\frac{n\hbar}{2} \end{align}$$

$$\begin{align} b_\text{max} &= j\hbar \\ b_\text{min} &= -j\hbar \end{align}$$

where $j = 0, \frac{1}{2}, 1, \frac{3}{2}, ...$ Recall that

$$\begin{align} c = b_\text{max}(b_\text{max}+\hbar) \end{align}$$

so we also have

$$\begin{align} c = j(j+1)\hbar^2 \end{align}$$

Now, we can insert these results back into the original eigenvalue equations for $\hat{M}^2$ and $\hat{M}_z$ to give

$$\begin{align} \hat{M}^2Y &= j(j+1)\hbar^2 Y\text{, }~~~j = 0, \frac{1}{2}, 1, \frac{3}{2}, ... \\ \hat{M}_z Y &= m_j \hbar Y\text{, }~~~m_j = -j, -j+1, ..., j-1, j \end{align}$$

Note that this is the same result as we obtained from explicitly solving the eigenvalue equations for the orbital angular momentum operators $\hat{L}^2$ and $\hat{L}_z,$ except that the quantum numbers $j$ and $m_j$ can take on half-integer values. The half-integer values would be rejected in the orbital angular momentum case because the associated wave functions would not satisfy the boundary conditions for the particle-on-a-sphere problem. It turns out that the half-integer quantum numbers are relevant for a different type of angular momentum, spin angular momentum, which is an intrinsic property of quantum mechanical particles.

Spin Angular Momentum¶

Spin angular momentum is an intrinsic property of microscopic particles, like their mass and charge. The concept of spin emerges in Dirac's relativistic extension of the Schrödinger equation. In non-relativistic quantum mechanics, spin is incorporated into a wave function because we know, from experiment, that quantum particles possess this property. Fundamental particles can be chategorized in one of two ways, based on their spin. Fermions have half-integer spin; for example, electrons are fermions with a spin quantum number, $s = \frac{1}{2}.$ Bosons have integer spin; for example, photons are bosons with $s = 1.$

Let us consider the spin of an electron, which is a fermion. All electrons have $s = \frac{1}{2},$ which determins the magnitude of the spin angular momentum, $s(s+1)\hbar^2 = \frac{3}{4}\hbar^2.$ From general chemistry, we learn that electrons can have $\alpha$ or $\beta$ spin, and we also refer to these electrons has having spin up or down. The terms "up" and "down" refer to the $z$ projection of the spin angular momentum, $m_s \hbar.$ From the analysis in the previous section, we know $m_s$ for an electron can take on two values. $\alpha$ spin electrons have $m_s = + \frac{1}{2},$ while $\beta$ spin electrons have $m_s = - \frac{1}{2}.$

The operators for spin angular momentum are analogous to those we considered above for orbital angular momentum. We have

$$\begin{align} \vec{S} &= \hat{S}_x \vec{i} + \hat{S}_y \vec{j} + \hat{S}_z \vec{k} \\ \hat{S}^2 &= \hat{S}_x^2 + \hat{S}_y^2 + \hat{S}_z^2 \\ \end{align}$$

These operators have the same commutator properties as we derived above for orbital angular momentum, so

$$\begin{align} [\hat{S}^2, \hat{S}_x] &= 0 \\ [\hat{S}^2, \hat{S}_y] &= 0 \\ [\hat{S}^2, \hat{S}_z] &= 0 \\ [\hat{S}_x, \hat{S}_y] &= i\hbar \hat{S}_z \\ [\hat{S}_z, \hat{S}_x] &= i\hbar \hat{S}_y \\ [\hat{S}_y, \hat{S}_z] &= i\hbar \hat{S}_x \\ \end{align}$$

Mathematically, we represent spin operators as

$$\begin{align} \hat{S}_x &= \frac{\hbar}{2} \sigma_x \\ \hat{S}_y &= \frac{\hbar}{2} \sigma_y \\ \hat{S}_z &= \frac{\hbar}{2} \sigma_z \end{align}$$

where $\sigma_x,$ $\sigma_y,$ and $\sigma_z$ are $2 \times 2$ Hermitian matrices called "Pauli spin matrices" and are defined by

$$\begin{align} \sigma_x &= \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} \\ \sigma_y &= \begin{pmatrix} 0 & -i \\ i & 0 \\ \end{pmatrix} \\ \sigma_z &= \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix} \\ \end{align}$$

The spin state of an electron can then be represented as a two-component vector quantity. We have

$$\begin{align} |\alpha \rangle &= \begin{pmatrix} 1 \\ 0 \end{pmatrix} \\ |\beta \rangle &= \begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ \end{align}$$

Are $|\alpha\rangle$ and $|\beta \rangle$ eigenfunctions (or eigenvectors) of the spin matrices? For $\hat{S}_x,$ we have

$$\begin{align} \hat{S}_x | \alpha \rangle &= \frac{\hbar}{2} \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} \\ &= \frac{\hbar}{2} \begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ &= \frac{\hbar}{2} |\beta\rangle \\ \hat{S}_x | \beta \rangle &= \frac{\hbar}{2} \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ &= \frac{\hbar}{2} \begin{pmatrix} 1 \\ 0 \end{pmatrix} \\ &= \frac{\hbar}{2} |\alpha\rangle \end{align}$$

For $\hat{S}_y,$ we have

$$\begin{align} \hat{S}_y | \alpha \rangle &= \frac{\hbar}{2} \begin{pmatrix} 0 & -i \\ i & 0 \\ \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} \\ &= \frac{\hbar}{2} \begin{pmatrix} 0 \\ i \end{pmatrix} \\ &= \frac{i\hbar}{2} |\beta\rangle \\ \hat{S}_y | \beta \rangle &= \frac{\hbar}{2} \begin{pmatrix} 0 & -i \\ i & 0 \\ \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ &= \frac{\hbar}{2} \begin{pmatrix} -i \\ 0 \end{pmatrix} \\ &= -\frac{i\hbar}{2} |\alpha\rangle \end{align}$$

For $\hat{S}_z,$ we have

$$\begin{align} \hat{S}_z | \alpha \rangle &= \frac{\hbar}{2} \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} \\ &= \frac{\hbar}{2} \begin{pmatrix} 1 \\ 0 \end{pmatrix} \\ &= \frac{\hbar}{2} |\alpha\rangle \\ \hat{S}_z | \beta \rangle &= \frac{\hbar}{2} \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ &= \frac{\hbar}{2} \begin{pmatrix} 0 \\ -1 \end{pmatrix} \\ &= -\frac{\hbar}{2} |\beta\rangle \end{align}$$

So, $|\alpha\rangle$ and $|\beta\rangle$ are not eigenfunctions of $\hat{S}_x$ or $\hat{S}_y,$ but they are eigenfunctions of $\hat{S}_z,$ with eigenvalues equal to $\frac{\hbar}{2}$ and $-\frac{\hbar}{2},$ respectively.

Are $|\alpha\rangle$ and $|\beta\rangle$ are eigenfunctions of $\hat{S}^2$? We have

$$\begin{align} \hat{S}^2|\alpha\rangle &= \hat{S}_x^2|\alpha\rangle + \hat{S}_y^2|\alpha\rangle + \hat{S}_z^2|\alpha\rangle \\ &= \frac{\hbar}{2}\hat{S}_x|\beta\rangle + \frac{i\hbar}{2}\hat{S}_y|\beta\rangle + \frac{\hbar}{2}\hat{S}_z|\alpha\rangle \\ &= \frac{\hbar^2}{4}|\alpha\rangle + \frac{\hbar^2}{4}|\alpha\rangle + \frac{\hbar^2}{4}|\alpha\rangle \\ &= \frac{3\hbar^2}{4}|\alpha\rangle \end{align}$$ and, similarly,

$$\begin{align} \hat{S}^2|\beta\rangle &= \frac{3\hbar^2}{4}|\beta\rangle \end{align}$$

So, both $|\alpha\rangle$ and $|\beta\rangle$ are eigenfunctions of $\hat{S}^2$, with eigenvalue $\frac{3\hbar^2}{4}.$

Lastly, note that a general spin function for an electron could be a linear combination of the $|\alpha\rangle$ and $|\beta\rangle$ spin functions, i.e.,

$$\begin{align} |g\rangle = c_1 |\alpha \rangle + c_2 |\beta\rangle \end{align}$$

where $c_1$ and $c_2$ are probability amplitudes whose square moduli are the respective probabilities that the electron would be found to have either spin up or down, if this property was measured.

Practice

Question 11.

Show that $$\begin{align}[\hat{S}^2, \hat{S}_x] &= 0 \\ [\hat{S}^2, \hat{S}_y] &= 0 \\ [\hat{S}^2, \hat{S}_z] &= 0 \\ [\hat{S}_x, \hat{S}_y] &= i\hbar \hat{S}_z \\ [\hat{S}_z, \hat{S}_x] &= i\hbar \hat{S}_y \\ [\hat{S}_y, \hat{S}_z] &= i\hbar \hat{S}_x \\ \end{align}$$

Question 12.

Find spin eigenfunctions of $\hat{S}_x$ and $\hat{S}_y.$ Are these eigenfunctions also eigenfunctions of $\hat{S}^2$?

Question 13.

Consider rasing and lowering spin operators

$$\begin{align} \hat{S}_\pm &= \hat{S}_x \pm i\hat{S}_y \\ \end{align}$$

Show that $$\begin{align} \hat{S}_+|\alpha\rangle &= 0 \\ \hat{S}_+|\beta\rangle &= \hbar|\alpha\rangle \\ \hat{S}_-|\alpha\rangle &= \hbar|\beta\rangle \\ \hat{S}_-|\beta\rangle &= 0 \end{align}$$

In [ ]: